Latent Dirichlet Allocation(LDA)
본 포스팅은 토픽모델링 기법중 하나인 LDA에 대해 포스팅 하도록 하겠습니다
LDA는 전체 문서집합에 대해 각 문서에 어떠한 토픽들이 존재하는지 보여주는 확률 모델로써, 각각의 문서는 여러개의 토픽을 지니며, 이산 자료들에 대한 확률적 생성모델로 주로 텍스트 자료들에 주로 사용됩니다 (Y.Wang et al., 2009). LDA의 각각의 문서는 여러 개의 토픽을 지닐 수 있다는 점에서 pLSA와 유사하지만, 토픽들이 디리클레 분포를 따른다고 가정합니다. 디리클레 분포는 연속 확률분포의 하나로 $k$차원의 실수 벡터중 벡터의 요소가 양수이며, 모든 요소를 더한값이 1인 경우에 정의되는 확률 분포입니다.
더 들어가보자면, 디리클레 분포는 베타 분포를 항이 여러 개인 경우로 확대한 것입니다. 서로 독립이며 각각이 감마 분포를 이루는 두 확률 변수 X1,X2X1,X2 로부터 베타 분포를 유도한 것처럼 감마 분포를 이루며 서로 독립인 k+1k+1 개의 확률 변수 X1,⋯,Xk+1X1,⋯,Xk+1 을 활용하여 디리클레 분포를 유도할 수 있습니다. 각각의 확률 변수를 다음과 같이 치환합니다.
$$ Y_1 = \frac{X_1}{\sum^{k+1}_{i=1}X_i}, Y_2 = \frac{X_2}{\sum^{k+1}_{i=1}X_i}, \cdots , Y_k = \frac{X_k}{\sum^{k+1}_{i=1}X_i}, Y_{k+1} = \sum^{k+1}_{i=1}X_i $$
이를 베타 분포에서 했던 것과 같은 과정을 거쳐 Y1,⋯,Yk+1Y1,⋯,Yk+1 의 결합 확률 분포 함수를 구한 뒤 이를 적분하여 확률변수 Y1,⋯,YkY1,⋯,Yk 의 결합 확률 분포 함수 gY1,⋯,Yk(y1,⋯,yk)gY1,⋯,Yk(y1,⋯,yk) 를 구할 수 있습니다. 이 때 Y1,⋯,YkY1,⋯,Yk 가 이루는 분포를 kk 차원 디리클레 분포라하며, Y1,⋯,Yk∼Dirichlet(α1,⋯,αk,αk+1)Y1,⋯,Yk∼Dirichlet(α1,⋯,αk,αk+1) 로 나타냅니다. 디리클레 분포의 수식은 아래와 같고 k=1k=1 일 때 베타 분포와 동일한 식을 가지게 됩니다.
$$g_{Y_1,\cdots,Y_k}(y_1,\cdots,y_k) = \frac{\Gamma(\sum^{k+1}_{i=1}\alpha_i)}{\prod^{k+1}_{i=1}\Gamma(\alpha_i)} \prod^{k+1}_{i=1} y_i^{\alpha_i-1} \\ (y_{k+1} = 1 - \sum^k_{i=1}y_i)$$
이러한 LDA는 토픽별 단어의 분포와 문서별 토픽의 분포를 추정할 수 있습니다.
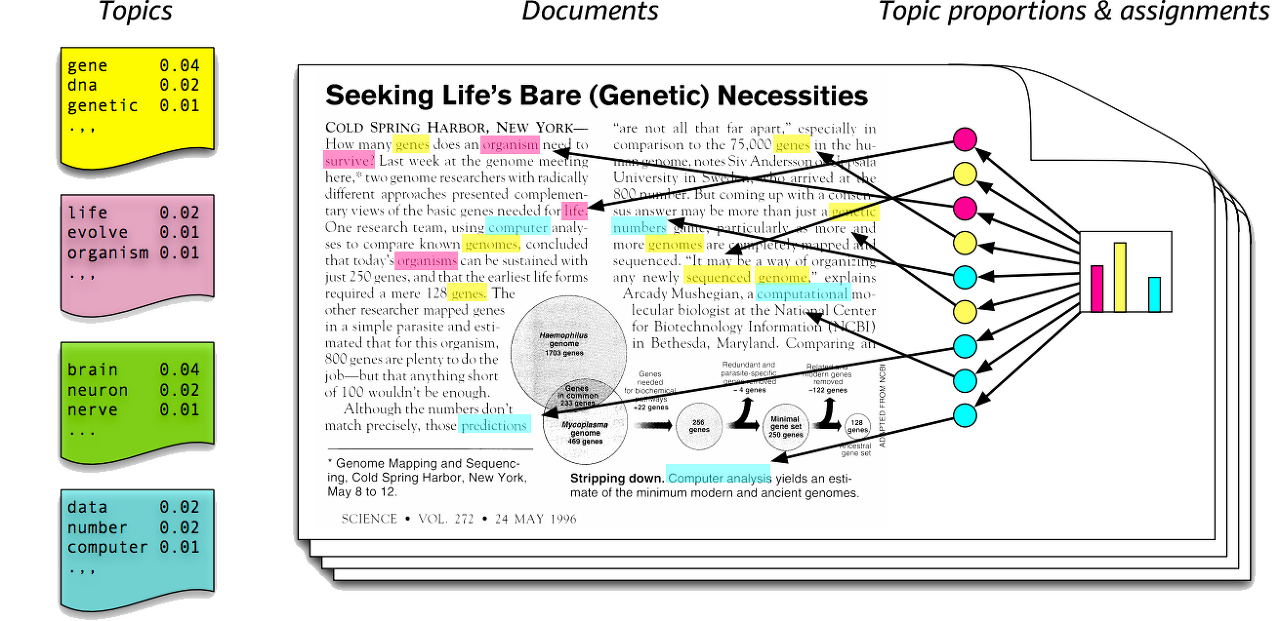
LDA는 특정 토픽에 내포될 특정 단어가 나타날 확률을 보여주는데, 위의 그림에서 총 4가지의 토픽 형성되어 진 것을 확인 할 수 있습니다. 위부터 노란색 토픽의 주요단어는 gene, dna, genetic으로 구성되며 이는 노란색 토픽이 gene에 대해 형성된 주제라는 것을 유추 할 수 있습니다.

위의 그림은 LDA모델에서 문서 생성 절차를 나타내었습니다. LDA는 D개의 문자가 주어져있고, 모든 문서가 K개의 토픽중 하나에 속할때 각 단어는 vocabulary index의 기본 단위로 표현 될 수 있습니다. 이때 vocabulary의 크기를 V라 하면 v∈{1,...,V}f로 표현이 가능합니다. 문서는 N개의 단어에 대한 시퀀스이며 w={w1,w2,w3,...,wn}으로 표현이 가능합니다. 말뭉치는 문서집합 M개 에 대한 모음으로 D={w1,w2,w3,...,wd}로 표현이 가능합니다. LDA는 가각의 문서 $w$∈$D$에 대해 아래와 같은 생성과정을 가정합니다.