| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
- 임베딩
- 알파베타가지치기
- 사회연결망분석
- 구글클라우드플랫폼
- ROC-AUC Curve
- sbert
- GCP
- Holdout
- 머신러닝
- Min-Max 알고리즘
- degree centrality
- topic modeling
- 의미연결망
- type-hint
- 분류모델평가
- hugging face
- sequential data
- word2vec
- 동적토픽모델링
- Google Cloud Platform
- semantic network
- 토픽모델링
- sensibleness
- 허깅페이스
- Enriching Word Vectors with Subword Information
- QANet
- 감성분석
- Meena
- dynamic topic modeling
- word representation
- Today
- Total
Dev.log
Graph centrality를 통한 금융 자연어 데이터 분석 본문
사회적 인식을 파악하기 위해 언론 보도를 토대로 언론의 시각에 의해 여론을 지각할 수 있는 연구들이 존재하였습니다. 또한, 인터넷의 보급화와 스마트 기기의 보급률 상승은 온라인 공간의 보편화를 이루어 내며 다양한 연령이 스마트 기기를 사 용하여 매체를 접하고 소비하는 시간이 증가시켰습니다. 이러한 온라인 공간의 보편화로 인해 온라인 공간에서의 담론은 대중의 인식을 추정할 수 있는 방법으로 사용할 수 있습니다.
이에 사회의 시스템구조를 파악하기 위해 사람, 사물, 조직 간의 관계를 네트워크 관점에서 분석하는 social network analaysis와 semantic network analysis가 등장하였습니다. Semantic network analysis은 social network analaysisfmf 커뮤니케이션 메시지에 적용시킨 방법으로 의제에 관해 거시적인 틀에서 분석할 수 있으며, 개별적인 키워드 위치와 역할을 파악함으로써 기존의 의제설정모델을 체계적으로 파악 할 수 있는 분석 방법입니다. 본 포스팅에서는 네이버 뉴스에서 '금융'이라는 키워드로 데이터를 수집후 TF-IDF x Cosin Simiarity로 형성된 matrix를 기반으로 그래프이론의 각 centrality로 노드간 가중치를 주어 시각화를 진행하여 semantic network analysis를 진행해 보도록 하겠습니다.
데이터 수집 및 전처리
데이터 수집 대상은 2022년 06월 01일 부터 2022년 06월 07일 까지, 총 7일간 네이버 뉴스에서 형성된 '금융'을 키워드로 수집하였습니다. 수집된 네이버 뉴스 데이터의 전처리 과정은 먼저 수집된 데이터에서 불필요한 특수문자(!,@,#,$)를 제거한 이후 PyKomoran을 통해 형태소 단위로 토크나이징을 진행하였습니다. 이때 PyKomoran내에서 제공하는 EXP 모델을 사용하였으며, EXP 모델의 경우 세종 말뭉치의 일부에 SHINEWARE에서 추가한 데이터를 이용하여 학습한 모델에서 추가적으로 Wikipedia의 문서 제목을 추가로 학습 시킨 모델입니다. 즉, EXP 모델은 뉴스나 SNS 분석과 같이 신조어 및 고유명사에 대해 학습이 되어있기 때문에 본 포스팅에서의 분석 대상인 네이버 뉴스에 적합하다고 판단되었습니다. 이후 토큰화된 데이터에서 한글자 이하의 단어들은 의미가 없다고 판단하여 제거하는 과정을 거쳤으며, 포괄적인 단어에 대해 단어의 빈도수에 따른 불용어 사전을 구축한뒤, 불용어 처리를 진행하였습니다. 이후 scikit-learnd을 통해 토큰화된 데이터들에 대해 cosin simiarity와 TF-IDF 값을 계산하였으며, 이를 바탕으로 메트릭스를 구축하는 전처리 과정을 거쳤습니다.
토큰화(tokenization)
자연어 처리에서 얻어낸 코퍼스 데이터가 필요에 맞게 전처리되지 않은 상태라면, 해당 데이터를 사용하고자하는 용도에 맞게 토큰화를 하게 됩니다. 아래의 데이터는 PyKomoran의 EXP 모델을 통해 형태소 단위로 토큰화를 진행시켰으며, 불용어 처리를 거치고 난 토크나이징된 데이터의 일부 입니다.

Cosin simiarity(코사인 유사도)
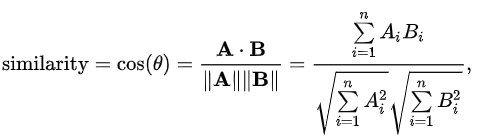
Cosin simiarity는 내적공간의 두 벡터간 각도의 cosin 값을 이용하여 측정된 벡터간 유사도를 의미합니다. 두 벡터의 방향이 완전히 동일한 경우에는 1의 값을 가지며, 90°의 각을 이루면 0, 180°로 반대의 방향을 가지면 -1의 값을 갖게 됩니다. 즉, 결국 코사인 유사도는 -1 이상 1 이하의 값을 가지며 값이 1에 가까울수록 유사도가 높다고 판단할 수 있습니다
TF-IDF
텍스트 분석에서 단어의 빈도(Term-Frequency)가 높을수록 중 요성이 높다고 가정하면 TF를 활용할 수 있습니다. 하지만 단어 자체가 한 개의 문서 내에서 자주 등장하는 경우에는 상투적인 단어로 전락되는 경우가 높으므로, 이러한 한계점을 극복하기 위해 TF-ID 지표를 사용 할 수 있습니다. TF-IDF는 다른 문서에서의 빈도수는 낮으며 해당 문서에서 등장하는 빈도가 높 은 단어들에게 높은 수치를 주어서 어떠한 단어가 특정 문서에 보이는 빈도가 높지 만 전체 문서에서의 출현 빈도가 낮은값을 부각 시킬 수 있습니다. 즉, TF-IDF의 값 을 사용하여 어떠한 단어가 문서에서 중요한 단어인지 파악 할 수 있게됩니다.

Network analysis
Cosin simiarity와 TF-IDF로 이루어진 matrix를 기반으로 시각화를 진행해 보도록 하겠습니다. 먼저 네트워크의 커뮤니티 구조는 얼마나 모듈화 되어있는지 알아보기 위해 커뮤니티 내부에 펼쳐져 있는 링크들이 무작위적인 연결들과 비교했을 때 얼마다 더 많은지 정량화를 한modualrity algorithim을 통해 군집을 구성하였습니다.
Modularity
odularity는 원래의 네트워크 G와 각 노드의 링크의 개수를 유지한 체로 대상을 랜덤하게 변화시킨 네트워크 G'와 원래 네트워크 G를 비교하여 도출되어집니다. 이러한 modularity의 기본 수식을 표현하면 아래와 같이 나타낼 수 있습니다.

여기서, Q는 모듈성을 의미하며, M은 전체 링크의수, N은 전체 노드의 수이며, a_ij는 i와 j간의 링크로, 링크가 존재할 경우는 1이고 없을 경우는 0으로 나타납니다. t_ij의 경우 각 노드가 지니는 링크의 갯수는 그대로 유지하며 대상을 무작위 적으로 재 연결 했을경우 노드 i와 j간의 링크로, 링크가 존재할경우는 1이며 존재하지 않을경우는 0으로 나타납니다, <t_ij>는 기대치를 의미하며 C(i)는 노드 i가 속하는 커뮤니티입니다. 위의 식을 살펴보면 커뮤니티 내부의 링크의 갯수가 무작위적 상태의 기대값 보다 얼마나 큰지를 알수있는데, 위식에서 <t_ij>값이 존재 하지 않다면 커뮤니티 내부의 링크의 수가 전체 링크 중 차지하는 비율을 나타내는 식이 됩니다. 즉 <t_ij>는 임의적 연결이 생성되는 modularity를 제거하기 위해 사용되었다 할수 있을것 같습니다. 무작위적인 상태로 정의한 링크 t_ij의 기대값을 구해보면 아래의 식으로 나타 낼 수 있습니다.

t_ij 는 각 node가 지닌 링크의 개수를 유지한 채로 무작위적으로 재구성한 network G'의 node i와 node j간의 link를 나타낸다. 링크가 있을 경우 1, 없을 경우 0의 값을 가집니다. 이 때, G'의 한 link가 node i와 node j간을 연결한 link일 확률은 (p_i * p_j + p_j * p_i) 입니다. 또한, 전체 link의 개수는 M이므로, t_ij의 기대값은 2*M*p_i*p_j로 나타낼 수 있습니다. p_i는 G'이 단순히 링크를 무작위적으로 재연결한 것이 아닌, 각 node가 지닌 link의 수를 유지하고 있다는 점에 주의해야 한다. 즉, 단순히 1/N (N: node 개수)의 확률이 아닌, node가 지닌 link의 수에 비례하는 확률을 이용해야 합니다. 이때 모든 노드의 링크의 수 k_i를 다 더하면 (2*전체 링크의 수(M))이 됩니다. 이는 한 링크는 양단에 연결된 두 노드에서 각각 더해지기 때문입니다.

이 식을 modularity Q를 구하는 식에 대입하면 modularity를 구하는 기본 식이 완성됨을 확인 할 수 있습니다.
Degree Centrality
Degree Centrality(연결 중앙성)은 하나로 인접한 노드들의 수를 이용해서 중앙성지표(centrality)를 측정하는 방법을 의미합니다. 즉 노드 A가 100개의 노드와 연결되어있고 노드 B에는 10개의 노드들이 연결되어있으면, 노드 A가 노드 B에 비해 많은 노드들과 연결되어 있으므로 중요하다고 판단합니다. 이러한 degree centrality는 두 노드의 연결 방향성에 따라 in-degree centrality와 out-degree centraliy로 나누어 질수 있습니다. 먼저 in-degree는 들어오는 링크의 수 또는 선행 노드의 수입니다. 그리고, out-degree는 나가는 링크의 수 또는 후속 노드의 수를 의미합니다.
Modularity와 degree centrality를 통한 시각화
이제 '금융'이라는 키워드로 데이터를 수집후 TF-IDF x Cosin Simiarity로 형성된 matrix를 기반으로 그래프이론의 degree centrality로 노드간 가중치를 주고 modularity로 노드간 군집을 형성한뒤 ForceAtalce2로 네트워크의 layout을 설정하여 시각화를 진행해 보았습니다.

'자연어처리' 카테고리의 다른 글
| Gensim의 Latent Dirichlet Allocation를 통한 분석 (0) | 2022.07.16 |
|---|---|
| Hugging Face의 Sentence Transformer (0) | 2022.06.11 |
| Sentence BERT (0) | 2022.05.11 |
| Bag of Words (0) | 2022.05.10 |
| 문서간 유사도: Jaccard Similarity & Cosine Similarity (0) | 2022.04.29 |
