| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- 허깅페이스
- sbert
- Enriching Word Vectors with Subword Information
- dynamic topic modeling
- 분류모델평가
- topic modeling
- QANet
- word representation
- 알파베타가지치기
- 토픽모델링
- Holdout
- GCP
- 머신러닝
- type-hint
- 동적토픽모델링
- 임베딩
- sequential data
- 의미연결망
- word2vec
- degree centrality
- semantic network
- hugging face
- Google Cloud Platform
- sensibleness
- 감성분석
- Min-Max 알고리즘
- Meena
- 구글클라우드플랫폼
- 사회연결망분석
- ROC-AUC Curve
- Today
- Total
Dev.log
DBSCAN - 밀도 기반 클러스터링 본문
본 포스팅에서는 밀도기반 클러스터링이라고도 불리는 DBSCAN(Density based spatial clustring of applications with noise)에 대해서 진행해 보도록 하겠습니다. DBSCAN은 19996년도의 A density-based algorithm for discovering clusters in large spatial database with noise 라는 논문에서 제시된 클러스터링 기법입니다. DBSCAN은 K-means와 같이 군집간의 거리나 중심을 이용한 클러스터링이 아닌 밀도를 통해 군집화를 하는 방법에 대해 제시를 하였는데, 이는 '동일한 클래스에 속하는 데이터는 서로 근접하게 분포할것이다' 라는 가정으로 동작하는 클러스터링이라 이해하면 될것 같습니다. 이러한 밀도기반 클러스터링과 중심기반 클러스터링에 대한 예시는 아래의 그림과 같습니다. 먼저 왼쪽그림의 경우 DBSCAN과 같이 밀도를 기반으로 클러스터링을 진행한 결과이며 오른쪽 그림의 경우 K-means와 같이 중심기반으로 클러스터링을 진행한 결과 입니다.
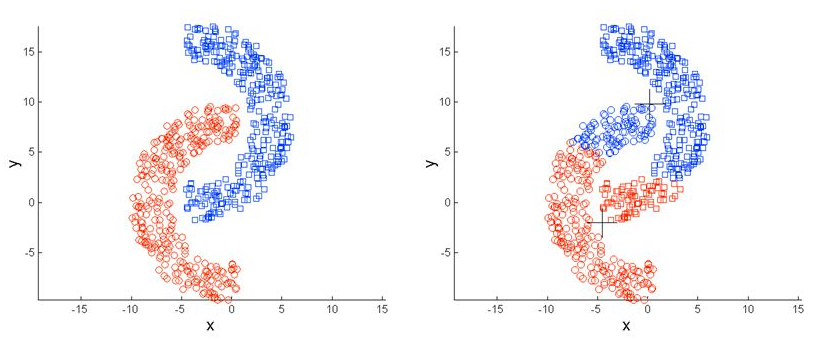
위의 그림과 같이 DBSCAN은 가깝게 모여있고 연결되어있는 데이터들에 대해 클러스터링을 진행할때 유용하게 사용될 수 있습니다. 또한 DBSCAN의 경우 클러스터의 갯수를 미리 정할 필요가없으며 노이즈에 대해 효과적으로 제외할 수 있습니다. 클러스터의 갯수를 정하지 않아도 된다는점은 처음 보는 데이터들에 대해 군집이 존재하는지 아니면 몇개의 군집이 존재하는지 알기 어려운 경우
DBSCAN의 작동방식은 반경의 크기와 최소 군집의 크기 두가지를 정해 준다음 클러스터링을 진행합니다. 반경의 크기는 데이터간의 거리가 얼마나 가까워야 서로 연결되어 하나의 군집으로 볼수 있는지를 의미하며 최소 근집의 크기는 몇개의 데이터가 서로 연결되어있어야 군집으로 볼건지를 의미합니다. 예를들어서 최소 군집의 크기인 MinPts가 5라면 4개의 데이터가 고르게 모여져있다고 해도 이를 노이즈로 간주하겠다는 의미입니다. 이러한 DBSCAN은 아래와 같이 작동한다고 볼 수 있습니다.
DBSCAN(DB, distFunc, eps, minPts) {
C := 0
for each point P in database DB {
if label(P) ≠ undefined then continue
Neighbors N := RangeQuery(DB, distFunc, P, eps)
if |N| < minPts then {
label(P) := Noise
continue
}
C := C + 1
label(P) := C
SeedSet S := N \ {P}
for each point Q in S {
if label(Q) = Noise then label(Q) := C
if label(Q) ≠ undefined then continue
label(Q) := C
Neighbors N := RangeQuery(DB, distFunc, Q, eps)
if |N| ≥ minPts then {
S := S ∪ N
}
}
}
}위의 의사코드를 간단하게 요약해 보자면, 먼저 랜덤하게 데이터포인트를 탐색합니다. 데이터 포인트를 탐색할때 마다 해당 포인트에서 다른 모든 데이터포인트까지의 거리를 계산하고, 미리 정한 반경의 크기(eps)보다 작은 데이터포인트가 MinPts - 1 이상만큼 존재한다면 해당 포인트는 core point 가 됩니다. 만일 아닐 경우 해당 포인트는 노이즈로 처리를 합니다. 그 후 모든 데이터포인트가 군집이거나 노이즈로 판단될때 까지 반복하는 과정이라 보면 될것 같습니다.
이러한 DBSCAN은 Python의 Scikit-learn 패키지를 통해 쉽게 사용할수있습니다.
sklearn.cluster.DBSCAN
Examples using sklearn.cluster.DBSCAN: Comparing different clustering algorithms on toy datasets Comparing different clustering algorithms on toy datasets, Demo of DBSCAN clustering algorithm Demo ...
scikit-learn.org
from sklearn.cluster import DBSCAN
import numpy as np
X = np.array([[1, 2], [2, 2], [2, 3],
[8, 7], [8, 8], [25, 80]])
clustering = DBSCAN(eps=3, min_samples=2).fit(X)Scikit-learn에서 제공하는 DBSCAN의 파라미터는 eps인 반경의 크기와 최소 군집의 크기인 min_samples를 필수적으로 설정해주어야하며 다른 파라미터의 경우 필수적으로 지정해 줄 필요는 없습니다. 먼저 제공해주는 파라미터에 대해 살펴보도록 하겠습니다
class sklearn.cluster.DBSCAN(eps=0.5, *, min_samples=5, metric='euclidean',
metric_params=None, algorithm='auto', leaf_size=30,
p=None, n_jobs=None)| 파리미터(Parameters) | 설명 |
| eps | 하나의 샘플에 대한 두 샘플 간의 최대 거리가 다른 샘플의 이웃으로 간주됩니다. 이것은 클러스터 내의 포인트 거리에 대한 최대 경계가 아닙니다. 이것은 데이터 세트 및 거리 기능에 대해 적절하게 선택하는 가장 중요한 DBSCAN 매개변수입니다. |
| min_samples | 핵심 포인트로 간주할 포인트에 대한 이웃의 샘플 수(또는 총 가중치)입니다. |
| metric | 피쳐 배열에서 인스턴스 간의 거리를 계산할 때 사용할 메트릭입니다. metric이 문자열이거나 호출 가능한 경우 해당 metric 매개변수에 대해 sklearn.metrics.pairwise_distances에서 허용하는 옵션 중 하나여야 합니다. metric이 "미리 계산된" 경우 X는 거리 행렬로 간주되며 정사각형이어야 합니다. X는 희소 그래프일 수 있으며, 이 경우 "0이 아닌" 요소만 DBSCAN의 이웃으로 간주될 수 있습니다. |
| metric_params | 메트릭 함수에 대한 추가 키워드 인수입니다. |
| algorithm | NearestNeighbors 모듈에서 포인트별 거리를 계산하고 가장 가까운 이웃을 찾는 데 사용할 알고리즘입니다. 자세한 내용은 NearestNeighbors 모듈 설명서를 참조하세요. |
| leaf_size | BallTree 또는 cKDTree에 전달된 리프 크기입니다. 이는 트리를 저장하는 데 필요한 메모리는 물론 구성 및 쿼리 속도에 영향을 줄 수 있습니다. 최적의 값은 문제의 특성에 따라 다릅니다. |
| p | 점 사이의 거리를 계산하는 데 사용되는 Minkowski 메트릭의 거듭제곱입니다. None이면 p=2(유클리드 거리와 동일)입니다. |
| n_jobs | 실행할 병렬 작업의 수입니다. None으로 설정할 경우 joblib.parallel_backend 컨텍스트가 아닌 한 1을 의미합니다. -1은 모든 프로세서를 사용함을 의미합니다. 자세한 내용은 용어집을 참조하십시오. |
DBSCAN은 군집의 갯수(=클러스터의 갯수)를 지정해 줄 필요가 없다는 점에서 장점을 가집니다. 하지만 여전히 eps와 같이 미리 설정해 주어야 하는 파라미터들이 존재합니다. 예를들어 eps를 너무 크게 설정해 버리면 모든 데이터들이 연결되어 버릴수 있으며, 작게 설정을 하면 모든 데이터들이 노이즈 처리가 될수 있습니다. 이러한 문제로 인해 DBSCAN을 사용할때 여러 값의 eps로 테스트를 해보면서 확인해 주어야 합니다.
'머신러닝과 딥러닝' 카테고리의 다른 글
| Hierarchical Clustering - 계층적 군집화 (0) | 2022.08.12 |
|---|---|
| DTW(Dynamic time wrapping) - 동적시간와핑 (0) | 2022.08.09 |
| Process Mining - 프로세스 마이닝 (0) | 2022.08.08 |
| ARIMA를 통한 시계열 데이터 분석 (0) | 2022.06.16 |
| Transfomer를 통한 시계열 데이터 예측 (5) | 2022.06.12 |



