| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
- sbert
- type-hint
- Google Cloud Platform
- Meena
- Enriching Word Vectors with Subword Information
- Holdout
- sensibleness
- QANet
- semantic network
- sequential data
- 동적토픽모델링
- word2vec
- degree centrality
- 토픽모델링
- 임베딩
- 구글클라우드플랫폼
- ROC-AUC Curve
- dynamic topic modeling
- Min-Max 알고리즘
- word representation
- 사회연결망분석
- 머신러닝
- topic modeling
- hugging face
- GCP
- 알파베타가지치기
- 의미연결망
- 감성분석
- 분류모델평가
- 허깅페이스
- Today
- Total
Dev.log
Hierarchical Clustering - 계층적 군집화 본문
Clustering(클러스터링) 혹은 군집분석이라고도 불리는 방법은 유사한 데이터들 끼리 그룹화를 시키는 비지도 학습이라고 할 수 있습니다. 클러스터링의 방법으로는 밀도기반 클러스터링인 DBSCAN, 중심기반인 K-means와 같은 다양한 방법들이 존재하며 이번 포스팅에서는 계층적 군집분석이라고도 불리는 hierarchical clustering에 대해서 진행해 보도록하겠습니다.
Hierarchical clustering이란
Hierarchical clustering은 데이터를 가까운 집단부터 순차적이며 계층적으로 군집화 하는 방식입니다. 즉, 트리구조를 통해 각 데이터들을 순차적, 계층적으로 비슷한 그룹과 묶어 클러스터링을 진행을 한다 라고 이해하면 될것 같습니다. 또한 계층적 구조로인해 DBSCAN과 마찬가지로 클러스터 혹은 군집의 갯수를 미리 정하지 않아도 됩니다. 다만 클러스터를 구성하는데 있어, 매번 local minimu을 찾아가는 방법을 활용하기때문에 클러스터링의 결과값이 global minimum이라고 해석하기는 어렵습니다.
Hierarchical clustering이 진행되는 과정은 먼저, 모든 데이터들 사이의 거리에 대한 유사도를 계산합니다. 그후 유사도가 비슷한 데이터들끼리 클러스터를 구성해주고, 유사도를 업데이트해주는 방식이라고 이해하면 될것 같습니다. Python에서는 Scipy에서 hierarchy 클러스터링 및 덴토그램을 통해 시각화 할 수있게 제공해줍니다.
Hierarchical clustering (scipy.cluster.hierarchy) — SciPy v1.9.0 Manual
These functions cut hierarchical clusterings into flat clusterings or find the roots of the forest formed by a cut by providing the flat cluster ids of each observation. fcluster(Z, t[, criterion, depth, R, monocrit]) Form flat clusters from the hiera
docs.scipy.org
import numpy as np
import matplotlib.pyplot as plt
from scipy.cluster.hierarchy import dendrogram, linkage
x = [4, 5, 10, 4, 3, 11, 14 , 6, 10, 12]
y = [21, 19, 24, 17, 16, 25, 24, 22, 21, 21]
data = list(zip(x, y))
linkage_data = linkage(data, method='ward', metric='euclidean')
dendrogram(linkage_data)
plt.show()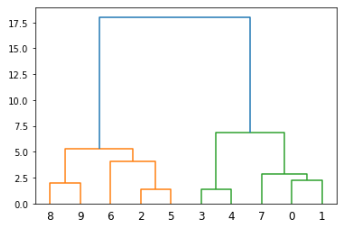
Hierachy clustering을 수행하는 코드 내 파라미터들에 대해서 살펴보겠습니다.
scipy.cluster.hierarchy.linkage(y, method='single',
metric='euclidean',
optimal_ordering=False)
Method
먼저 y의 경우 인풋값으로 1-D나 2-D의 백터형태로 들어갑니다. 즉, 클러스터링을 진행하고자 하는 데이터의 인풋에 대한 파라미터입니다. 이후 method는 새로 형성된 클러스터와 각각의 클러스터 사이의 거리를 계산하는 방법에 대한 파라미터 입니다. 즉, K-means와 같이 거리를 설정할 수 있는 파라미터라 이해하면 될것같습니다. 거리는 크게 single, complete, average, 그리고 weighted로 나누어집니다.
Single은 각 클러스터내 데이터 사이의 가장 짧은 거리를 통해 계산하는 방식입니다. 즉, 가장 비슷한 두 데이터의 거리를 두 클러스터의 거리로 정의합니다. Complete는 각 클러스터내 가장 긴 거리를 두 클러스터간 거리로 생각하여 가장 비슷하지 않은 두데이터의 거리를 클러스트간의 거리로 판단하는 방식입니다. Average는 클러스터내 모든 데이터의 거리의 평균을 두 클러스터 사이의 거리로 판단합니다. Centroid의 경우 각 클러스터의 중앙값 사이의 거리를 두 클러스터간의 거리로 판단합니다.
이들을 식으로 표현하면 아래와 같이 나타낼 수 있습니다.
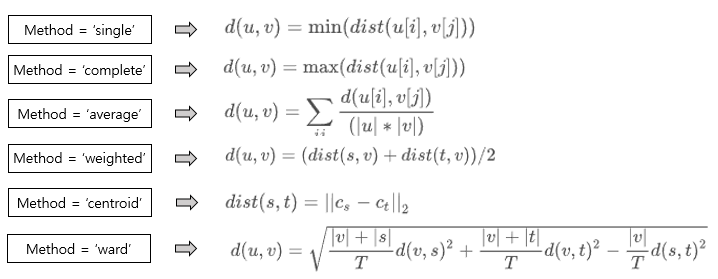
이를 그림으로 표현해보면 다음과 같습니다.
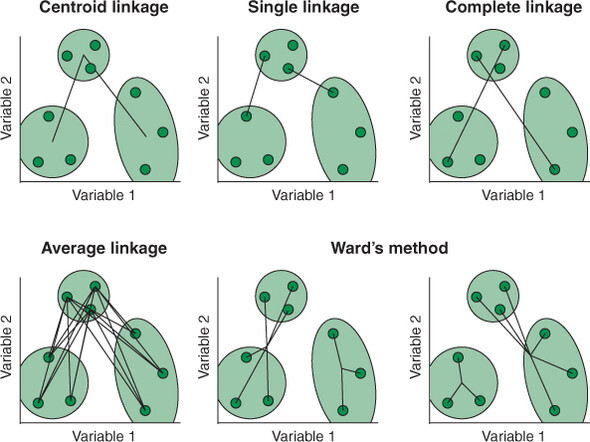
Metric
Distance metric의 경우 대표적으로 euclidean, manhattan, minkowski, cosin 등이 존재합니다. 본 포스팅에서는 간단하게 distance metric에 대해 정리해보겠습니다. 먼저, Euclidean distance는 공간에서 두 점 사이를 지나는 선분의 길이를 측정하여 두 점 사이의 거리를 계산하는 방식이며 이를 식으로 표현하면 다음과 같습니다.
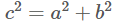
Manhattan distance는 두 점의 모든 차원에서 측정값 간의 절대 차이의 합입니다. 그 차원이 2이면 한 블록을 걸을 때 오른쪽과 왼쪽을 만드는 것과 유사합니다.
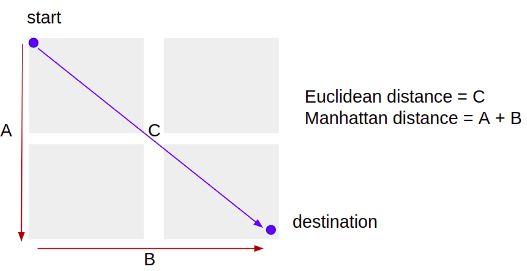
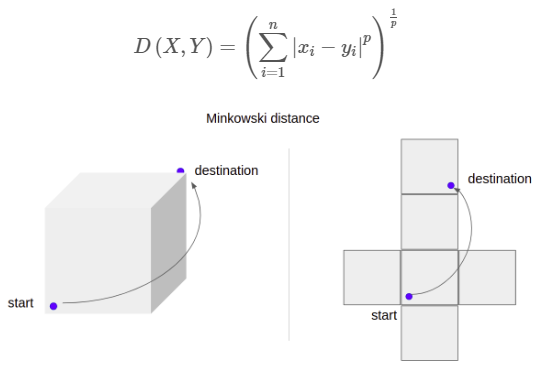
Minkowski distance는 euclidean distance와 Manhattan distance의 일반화라 볼 수 있습니다. Minkowski 미터법 p의 차수에 대한 절대 차이를 기반으로 거리를 계산하는 방법입니다. p > 0에 대해 정의되지만 1, 2 혹은 무한대 이외의 값에는 거의 사용되지 않습니다. Minkowski distance는 p=1일 때 Manhattan distance와 같고, p=2일 때 euclidean distance와 같습니다.
Cosin의 경우는 두 개의 점 시퀀스 또는 벡터 사이의 코사인각도에 대한 거리입니다. 코사인 유사도는 벡터의 내적을 길이의 곱으로 나눈 값입니다.
Hierarchical clustering을 통한 소비 데이터셋 군집화
이제 데이터셋을 가지고 hierarchical clustering을 진행해 보도록하겠습니다. 클러스터링에 들어가기앞서, 주어진 데이터셋에 대해 간단히 EDA를 진행해 보도록 하겠습니다.
import pandas as pd
df = pd.read_csv('D:/code/shopping-data.csv')
print(df.shape)
print(df.columns)
df['Spending Score (1-100)'].hist()
>>> (200, 5)
>>> Index(['CustomerID', 'Genre', 'Age', 'Annual Income (k$)',
'Spending Score (1-100)'],
dtype='object')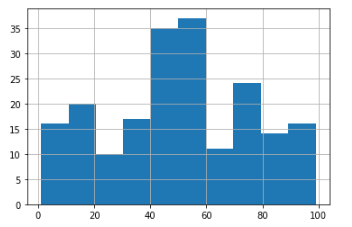
데이터셋을 보면 총 200명의 고객 각각에 대해 1에서 100까지의 지출 점수를 수집한 것을 볼 수 있습니다. 지출 점수의 값은 1에서 100까지의 척도에서 한 사람이 쇼핑몰에서 돈을 지출하는 빈도를 의미합니다. 즉, 고객의 점수가 0이면 이 사람은 절대 지출하지 않으며 점수가 100이면 가장 많이 지출한 사람입니다.
더불어, 히스토그램을 보면 35명 이상의 사람이 40점에서 60점 사이의 점수를 갖고 25명 미만이 70에서 80 사이의 점수를 가짐을 알 수 있습니다. 따라서 대부분의 사람은 소비에 있어 합리적이며 그 다음이 소비 지출이 많은 사람임을 알 수 있습니다. 또한 0과 100에 대한 공백은 분포에 지출을 하지 않은사람은 포함되지 않고 100점을 받을 만큼의 고소비자도 없음을 의미할 수 있습니다.
df.describe().transpose()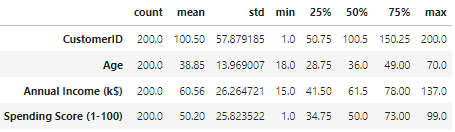
또한 지출 점수의 최소값은 1이고 최대값은 99입니다. 따라서 0 또는 100개의 점수 지출자가 없습니다. 또한 평균과 표준편차를 살펴보면 Age의 경우 평균이 38.85이고 표준편차가 약 13.97임을 알 수 있습니다. 연간 소득의 경우 평균이 60.56이며 표준편차는 26.26이고 spending score는 평균이 50이고 표준이 25.82으로 확인 할 수 있습니다. 평균이 표준 편차에서 멀리 떨어져 있는경우 데이터의 변동성이 높다는 것을 나타냅니다. Auunal Income에 대해 히스토그램을 그려보면 다음과 같이 나타납니다. 해당 히스토그램에서는 오른쪽으로 갈때 데이터의 변화가 급변한다는 점을 확인 할 수 있습니다.
df['Annual Income (k$)'].hist()
또한 성별에 대한 비율을 확인해보면 여성이 56%, 남성이 44%로 구성되어있는것을 알 수 있습니다.
df['Genre'].unique()
df['Genre'].value_counts(normalize=True)
>>> Female 0.56
>>> Male 0.44
>>> Name: Genre, dtype: float64더불어 연령대를 그룹화해서 연령대에 대해 살펴보겠습니다. 연령대는 총 15세부터 20세, 20세 부터 30세, 30세 부터 40세, 40세 부터 50세, 50세부터 60세, 그리고 60세 부터 70세 까지 그룹화를 진행해보았습니다.
grps = [15, 20, 30, 40, 50, 60, 70]
col = df['Age']
df['Age Groups'] = pd.cut(x=col, bins=grps)
df.groupby('Age Groups')['Age Groups'].count()
Age Groups
(15, 20] 17
(20, 30] 45
(30, 40] 60
(40, 50] 38
(50, 60] 23
(60, 70] 17
Name: Age Groups, dtype: int64이제 클러스터링 분석을 위해 먼저 Seaborn 패키지 내 pairpolot을 통해 데이터를 시각화해 보겠습니다. Customer ID의 경우 분석에 필요하지않음으로 제거를 해준뒤 진행해 주었습니다. Pairplot(산점도)를 통해 데이터를 확인해보면 데이터 그룹이 있는 것처럼 보이는 산점도를 찾을 수 있습니다. 또한 해당 산점도는 연간 소득과 지출 점수를 결합한 산점도임을 알 수 있습니다. 반면 다른 변수들의 산점도 사이에는 명확한 구분이 없음을 확인 할 수 있습니다.
import seaborn as sns
data = df.drop('CustomerID', axis=1)
sns.pairplot(data)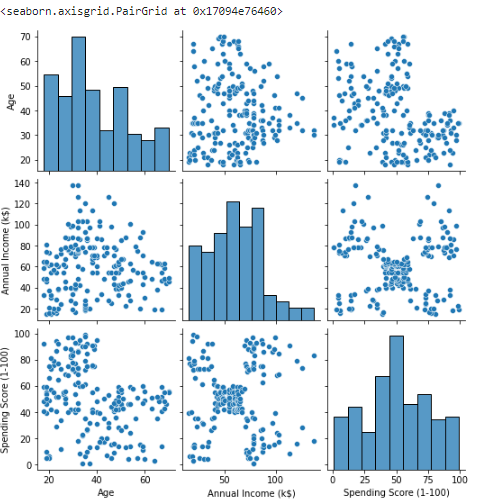
따라서, Annual Income과 spending score로 구성된 두 산점도를 scatterplot을 사용하여 확인해 보았으며 총 5개의 그룹이 구성된다고 유추 할 수 있습니다
sns.scatterplot(x = data['Annual Income (k$)'],
y = data['Spending Score (1-100)'])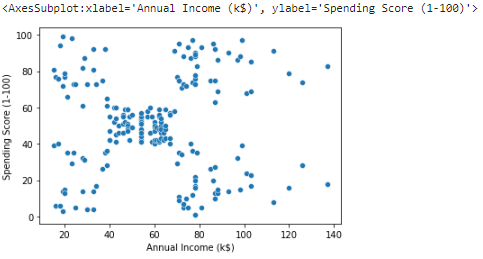
이제 Annual Income과 spending score에 대해 hierachy clustering을 진행해 보도록 하겠습니다. 클러스터링의 시각화는 덴토그램을 통해 진행하였으며 method는 ward, 그리고 metric은 유클리드 거리를 통해 클러스터링을 진행하였습니다.
import scipy.cluster.hierarchy as shc
import matplotlib.pyplot as plt
plt.figure(figsize=(10, 7))
plt.title("Dendrogram")
# Selecting Annual Income and Spending Scores by index
input_data = data.iloc[:, 2:4]
clusters = shc.linkage(input_data,
method='ward',
metric="euclidean")
shc.dendrogram(Z=clusters)
plt.axhline(y = 130, color = 'r', linestyle = '-')
plt.show()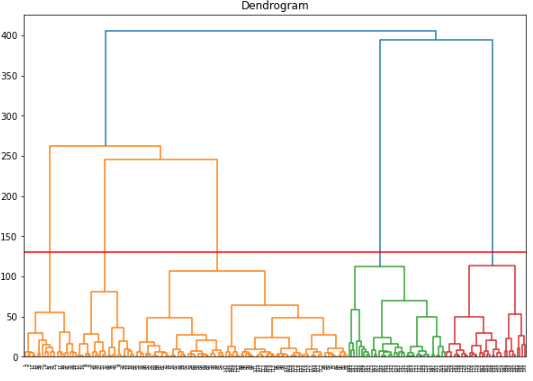
Hierachy clustering을 통해 5개의 군집에 대해 확인 이후 군집의 수를 5로 설정한뒤에 Agglomerative Clustering을 사용하여 레이블링을 진행해 보겠습니다. 0부터 4까지의 총 5개의 군집으로 데이터가 군집화 된것을 확인 할 수 있습니다.
from sklearn.cluster import AgglomerativeClustering
clustering_model = AgglomerativeClustering(n_clusters=5, affinity='euclidean', linkage='ward')
clustering_model.fit(input_data)
data_labels = clustering_model.labels_
sns.scatterplot(x='Annual Income (k$)',
y='Spending Score (1-100)',
data=input_data,
hue=data_labels,
palette="Paired").set_title('Labeled Data')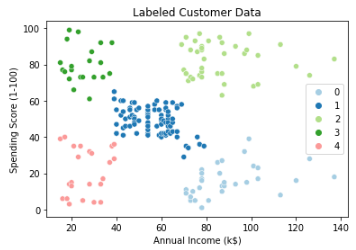
'머신러닝과 딥러닝' 카테고리의 다른 글
| DTW(Dynamic time wrapping) - 동적시간와핑 (0) | 2022.08.09 |
|---|---|
| DBSCAN - 밀도 기반 클러스터링 (0) | 2022.08.08 |
| Process Mining - 프로세스 마이닝 (0) | 2022.08.08 |
| ARIMA를 통한 시계열 데이터 분석 (0) | 2022.06.16 |
| Transfomer를 통한 시계열 데이터 예측 (5) | 2022.06.12 |



